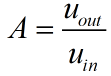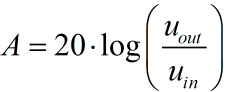RC-Led

Et RC-Led kan betragtes som en frekvensafhængig spændingsdeler. Det betyder at man kan lade et signal over eller under en bestemt frekvens passere rimeligt uhindret, mens signalet under eller over bliver dæmpet i en vis grad. Man kan lave to forskellige typer RC-led, et højpasfilter og et lavpasfilter.

Lavpas filter

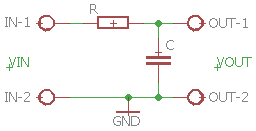
Lavpasfilter, hvor udgangspændingen tages ud over kondensatoren

Frekvensgangen for et Lavpasfilter

I pasbåndet under overgangsfrekvensen passerer signalet rimeligt uhindret gennem filteret - altså 0 dB mellem indgang og udgang. I overgangsfrekvensen dæmper RC-leddet 3 dB. RC-leddene har et fald på 6 dB pr. oktav (fordobling af frekvens) og 20 dB pr. dekade (frekvens gange 10).

Højpas filter

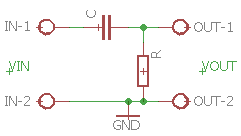
Højpasfilter, hvor udgangspændingen tages ud over modstanden

Frekvensgangen for et Højpasfilter

I pasbåndet over overgangsfrekvensen passerer signalet rimeligt uhindret gennem filteret - altså 0 dB mellem indgang og udgang. I overgangsfrekvensen dæmper RC-leddet 3 dB. RC-leddene har en stigning på 6 dB pr. oktav (fordobling af frekvens) og 20 dB pr. dekade (frekvens gange 10).

Forskellen på høj og lav-pasfilteret er altså hvor man tager signalet ud. Spændingen bliver fordelt over modstanden og kondensatoren. Spændingsfaldet over kondensatoren er afhængig af forholdet mellem kondensatorens reaktans og størrelsen på modstanden R. Da kondensatorens reaktans er afhængig af frekvensen bliver spændingsfordelingen afhængig af frekvensen. Ved høje frekvenser bliver X_C lille og derfor bliver spændingsfaldet over R større. Ved lav frekvens bliver X_C stor og spændingsfaldet over R lille.

Overgangsfrekvens

Overgangsfrekvensen er vigtigt når vi taler om filtre. Den bliver også kaldt for cut-off frekvensen, f₀. Det er den frekvens der afgør om der er tale om høje eller lave frekvenser. Overgangsfrekvensen er den frekvens hvor R=X_C. Den frekvens kan findes ved at indsætte formlen for X_C.

Ud fra dette kan man finde frem til overgangsfrekvensen som er:

Dette giver ikke hele billedet, men man kan læse mere ved at betragte komponenterne ved hjælp af Komplekse tal

Forstærkning

Forstærkning i et RC led kan bergenes med denne formel:

Det kan være en fordel at regne forstærkningen i dB, det gør man med denne formel:

RC-led og firkantspænding

Hidtil har vi kigget på RC-led ved sinus spændinger. Hvis vi tilfører en firkant spænding vil der skiftevis være en opladning og en afladning, som vil ændre firkantspændingens kurvefom.

Intergrationsled

Kobles RC-leddet som et lavpasled har man et integrationsled. Integrationsleddet leverer en udgangsspænding der er lige med indgangsspændingens middelværdi. Et godt integrationsled kræver at tidskonstanten τ er mindst 10 gange større end spændingsepriodetiden. Hvis τ gøres større vil udsvingene i spændingen blive mindre og efterhånden bliver spændingen til en næsten jævn DC-spænding, som ligger på middelværdien af pulsen. Der vil gå lidt tid inden kondensatoren bliver ladet op til middelværdien, den tid kaldes indsvingningstiden.

Differentiationsled

Kobles et Højpasled har man et differentiationsled. Et differentiationsled overfører kun forskellene i spændingerne. Differentiationsleddet leverer en udgangsspænding der er udtryk for ændringen i indgangsspændingen. Når indgangsspændingen stiger, får vi en positiv spændingsspids og tilsvarende når spændingen falder får vi en negativ spændingsspids. Differentiationsleddet bruges til at lave styreimpulser eller triggerimpulser. Et godt differentiationsled har en tidskonstant τ der er mindst 100 gange mindre end spændingens periodetid. Det sikrer at impulserne bliver korte ”nåle-impulser”. Hvis tidskonstanten τ stiger bliver impulserne længere, for til sidst at minde om indgangsspændingen.

Filtre
Filtre	Aktive filtre - Komplekse tal - Sammenkobling af filtre - Butterworth - Chebyshev - Band-pass - RC-Led - Spole ved AC