Butterworth filtre

Butterworth filtre er klassiske filtre, der har gode signalbehandlingsegenskaber, og som er relativt enkle at opbygge, men som heller ikke afskærer så hårdt som andre filtertyper. Man kan realisere Butterworth filtre på forskellig vis. Det klassiske ved Butterworth er at man lægger knækfrekvensen samme sted. På denne måde vil man typisk få en flad overgangs-kurve, der har -3dB ved knækfrekvensen. Filtertypen har flere fordele, bl.a. at den har en bedre fase karakteriistik, men den giver ikke det samme stopbånd, som andre typer filtre. Placerer man derimod forskellige toppe lige omkring knækfrekvensen, så de kompenserer for hinanden, så kan man få et stejlere filter i transitionsbåndet, og man kan få mindre dæmpning i knækfrekvensen. Prisen for dette er så til gengæld at der kommer bølger i pasbåndet, som ved et Chebyshev filter.

Filtre Aktive filtre Band-pass filter Butterworth filtre Chebyshev filtre Komplekse tal RC-Led Sammenkobling af filtre Spole ved AC

Realisering af Butterworth filtre generelt

Butterworth filtre realiseres ud fra en række polynomier er der defineret i s-området som følger:

Polynomierne fra s-området til Butterworth filtre op til 8. orden

Det man kan se her er, at de ulige ordner (1. 3. 5. osv) har et 1. ordens led som et af elementerne, og så er der ellers koblet flere andenordens led sammen, men da konstanten på s² alle steder er på 1, så ligger de på samme knækfrekvens, men har forskellige Q, som definerer komponentværdierne.

Beregninger på et 2. ordens led

Der er forskellige måder at realisese 2. ordens led på, men her tages udgangspunkt i et Sallen-Key med unity gain, som ser således ud i et lavpas filter:

Diagrammet til et SallenKey Lavpas filer

For at beregne komponenterne skal man bruge konstanten fra ^s1 leddet, der for et 2. ordens filter hedder K=1.4142.

Man skal også vælge en kondensator, som forsøges valgt ud fra hvilke frekvenser man arbejder med, men også ud fra praktiske hensyn, så man får en kondensator til en fornuftig pris. Herefter kan de resterende komponenter beregnes ud fra følgende:

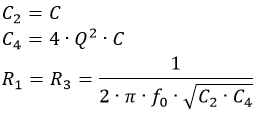
Formler til beregning af Sallen-Key Lavpas filter

Tilsvarende kan man realisere et højpas filter med et Sallen-Key filter på følgende måde:

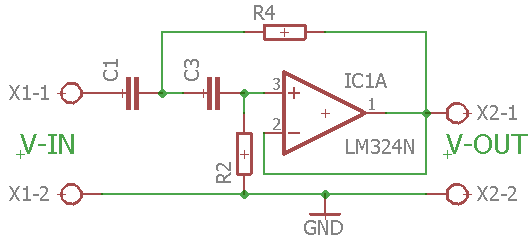
Diagrammet til et SallenKey Højpas filter

Man vælger igen kondensatoren først, da kondensatorer ikke fås i så mange forskellige størrelser (i hvert fald ikke til en fornuftig pris), og man anvender samme K fra s-udtrykket. Dette giver følgende beregninger:

Formler til beregning af Sallen-Key Højpas filter

Opbygning af 5. ordens filter

For at realisere et 5. ordens filter skal det bestå af 3 filtre efter hinanden, et 1. ordens og to 2. ordens, så den samlede orden bliver til 5. orden.

Det gennemregnede eksempel på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen 5orderButterworth.mw.

Realisering af 5. ordens lavpas Butterworth

Der vælges en forstærkning på 1, fordi hele filteret realiseres med Sallen-Key filtre og simple 1. ordens filtre. Der vælges en knækfrekvens på 3,3 kHz

Der tages udgangspunkt i s-udtrykket for et 5. ordens, hvor det vi skal bruge er de to konstanter:

Polynomiet til et 5. ordens Butterworth filter

Konstanterne til et 5. ordens Butterworth filter

Første led - det 1. ordens filter

Første led realiseres med et 1. ordensfilter på knækfrekvensen

Førsteordens lavpasfilter

Beregningerne på filteret er som følger:

Beregningerne til det første filter

Andet led - det første 2. ordens filter

Det næste led realiseres med et 2. ordens Sallen-Key filter, det dimensioneres ud fra den angivne procedure, igen lige på knækfrekvensen og med K1 som den konstant der anvendes.

Diagrammet til et SallenKey Lavpas filter

Der lægges 10 til komponentnavnene i det første filter

Beregningerne til det andet filter

Tredje led - det andet 2. ordens filter

Ud fra den anden konstant K2 beregnes på samme måde et andet 2. ordens Sallen-Key filter:

Diagrammet til et SallenKey Højpas filter

Der lægges 20 til komponentnavnene i det første filter

Beregningerne til det tredje filter

Kontrol af filteret

For at vise hvordan funktionerne spiller sammen laves et plot, hvor de 3 funktioner indgår:

Graf med de 3 led til det 5. ordens Butterworth filter

På noget der ligner samme skala laves det samlede plot af den endelige funktion A(f), der er de 3 funktioner ganget sammen:

Graf med det samlede 5. ordens Butterworth filter

Som det kan ses på grafen, så udfylder den fint den ønskede funktion, at der dæmpes kraftigt med stigende frekvens, og at frekvensgangen i pasbåndet er helt flad. For at eftervise at dæmpningen i knækket også ligger som forventet beregnes denne:

Kontrol af det samlede Butterworth filters 3 dB punkt

Det gennemregnede eksempel på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen 5orderButterworth.mw.

Referencer

Filtre
Filtre	Aktive filtre - Komplekse tal - Sammenkobling af filtre - Butterworth - Chebyshev - Band-pass - RC-Led - Spole ved AC