Aktive filtre

Aktive filtre kaldes aktive, fordi de indeholder et aktivt element, typisk en operationsforstærker der hjælper signalbehandlingen, og som kan tilføje nogleekstra egenskaber til filtrene, som er svære at opnå med passive filtre, specielt uden anvendelse af spoler.

Filtre Aktive filtre Band-pass filter Butterworth filtre Chebyshev filtre Komplekse tal RC-Led Sammenkobling af filtre Spole ved AC

Første ordens filtre

Første ordens filtre er normalt bare lavet ved hjælp af et RC-Led, og nærmere beskrivelse af beregninger på dem er også beskrevet under komplekse tal.

Et simpelt RC-led er et passivt filter. Funktionen af et 1. ordens aktivt filter er præcist den samme, bortset fra at det aktive filter ikke er følsomt over for belastninger, som det er eftervist under sammenkobling af filtre.

Typisk vil 1. ordens filtre være lavet enten omkring en inverterende forstærker eller en ikke inverterende forstærker eller evt. den specielle ikke invertrende forstærker, der kun har 1 gangs forstærkning en spændingsfølger, som de ses herunder:

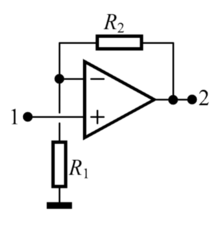Ikke inverterende forstærker

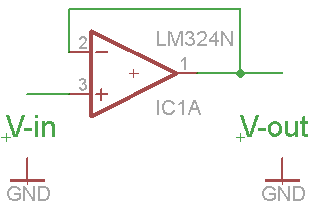Spændingfølger 1 gangs forstærkning

Inverterende forstærker

Filter-muligheder på en spændingsfølger

Et eksempel på et aktivt 1. ordens filter på en spændingsfølger ses herunder:

Førsteordens højpasfilter

Et aktivt lavpasfilter laves på samme måde, blot med et passivt lavpasfilter i indgangen i stedet for højpasfilteret som vist her:

Førsteordens lavpasfilter

Filter-muligheder på en ikke inverterende forstærker

På den ikke inverterende forstærker kan man placere 1. ordens led på samme måde som ved spændingsfølgeren, hvilket vil give samme filterfunktion. Ud over dette kan man erstatte begge modstande med et RC-led, enten i serie eller i parallel. Dette er dog ikke helt uden komplikationer.

Ved at placere en serieforbindelse i stedet for modstanden R1 der går til stel kan man få højpasfilter som vist her:

Førsteordens højpasfilter med pasbåndsforstærkning

Det viste filter har en pasbånds-forstærkning bestemt af R2 og R1, og en DC-forstærkning på 1 gang, så forstærkningen går ikke mod 0.

Placerer man i stedet en parallel-forbindelse af en kondensator og en modstand i stedet for R2, så får man et lavpas-filter som vist her:

Førsteordens lavpasfilter med pasbåndsforstærkning

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen firstOrderAktive.mw.

Dårlige kombinationer på den ikke inverterende forstærker

De viste kombinationer fungerer godt.

Man kan også erstatte R1 med en parallel-forbindelse af en kondensator og en modstand, men det vil have den ulempe at jo højere frekvensen bliver, jo højere vil forstærkningen blive, så forstærkningen vil i praksis gå mod uendeligt, hvilket dels ikke kan lade sig gøre, og dels vil det ganske givet give selvsving.

Det kan også lade sig gøre at erstatte R2 med en serieforbindelse, men det vil have den uheldige virkning, at den ikke bliver DC-stabil, så den vil stille og roligt drive ud mod den positive eller den negative begrænsning, så kredsløbet vil komme til at forvrænge.

Filter-muligheder på en inverterende forstærker

På den inverterende forstærker kan man erstatte begge modstande med et RC-led, enten i serie eller i parallel. Dette er dog ikke helt uden komplikationer.

Ved at placere en serieforbindelse i stedet for modstanden R1 der sidder i indgangen kan man få højpasfilter som vist her:

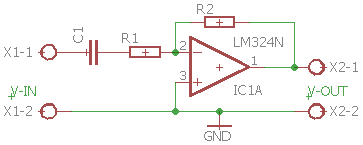
Førsteordens højpasfilter med pasbåndsforstærkning

Det viste filter har en pasbånds-forstærkning bestemt af R2 og R1, og en DC-forstærkning på 0 gange, da kondensatoren adskiller DC.

Placerer man i stedet en parallel-forbindelse af en kondensator og en modstand i stedet for R2, så får man et lavpas-filter som vist her:

Førsteordens lavpasfilter med pasbåndsforstærkning

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen firstOrderAktive.mw.

Dårlige kombinationer på den inverterende forstærker

De viste kombinationer fungerer godt.

Man kan også erstatte R1 med en parallel-forbindelse af en kondensator og en modstand, men det vil have den ulempe at jo højere frekvensen bliver, jo højere vil forstærkningen blive, så forstærkningen vil i praksis gå mod uendeligt, hvilket ikke kan lade sig gøre. Filteret vil desuden komme til at belaste meget hårdt på det foranliggende trin, så det vil også få indflydelse på frekvensgangen, og det vil ikke fungere efter hensigten.

Det kan også lade sig gøre at erstatte R2 med en serieforbindelse, men det vil have den uheldige virkning, at den ikke bliver DC-stabil, så den vil stille og roligt drive ud mod den positive eller den negative begrænsning, så kredsløbet vil komme til at forvrænge.

Kombinationer til Båndpas-filtre

På den ikke inverterende forstærker kan man kombinere de to filtre til et båndpas-filter som vist her:

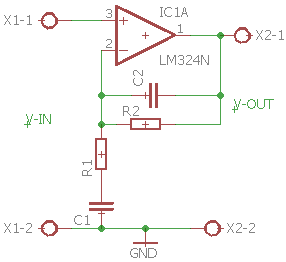
Båndpasfilter lavet med to Førsteordens filtre

Det samme kan man gøre på den inverterende forstærker, så man får et båndpas-filter som vist her:

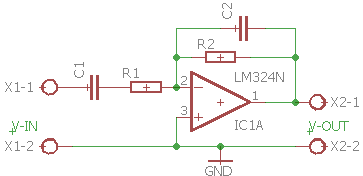
Båndpasfilter lavet med to Førsteordens filtre

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen firstOrderAktive.mw.

Anden ordens aktive filtre

I det 1. ordens filter ligger det frekvensbestemmende element før operationsforstærkerens indgang, og det eneste operationsforstærkeren gør er at gengive signalet, bare med en effekt bag, så signalet kan belastes, uden at det ændrer sig.

I de forskellige typer 2. ordens filtre kan man ikke nøjes med at realisere filteret før operationsforstærkeren, med mindre man vil bruge både kondensatorer og spoler, hvilket ikke er hensigtsmæssigt, da spoler er dyrere og samtidigt ikke særligt præcise, så derfor er det praktisk kun at anvende modstande og kondensatorer. Det kræver at man anvender signalet fra udgangen og kobler noget af det tilbage til indgangen via kondensatorer eller modstande.

Den tilbagekobling man laver gør at man kan få filteret ikke til bare at dæmpe et område, men specielt omkring knækfrekvensen kan man få et større eller mindre løft (måske ligefrem en peak).

Den "rigtige" filterdesign vil kræve en forståelse af s-planet, som det anvendes i FilterDesignTechniques, men man kan komme rigtigt langt med en god fornemmelse af den ønskede frekvensgang, nogle håndregler omkring filtrene, og så regne sig igennem til filtrenes frekvensgang med Maple.

Der er mange forskellige filteropbygninger, der kan realisere det samme, men to klassikere er Sallen-Key konfiguration og multiple feedback konfiguration - begge kan lave Highpass, Lowpass og båndpass ved at skifte modstande ud med kondensatorer.

Sallen-Key Filtre

Det generelle layout for sådan et filter ser ud som følger:

Generel layout for et Sallen-Key Filter - impedanserne er modstande eller kondesatorer

Ved reduktion af udtrykket for de generelle impedanser kan man komme frem til følgende udtryk for forstærkningen:

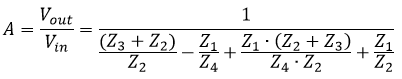
Generelt udtryk for et Sallen-Key filter

Reduktionerne der er lavet for at beregne det generelle udtryk er lavet i PDF-filen andenOrdensReduktion, hvor dette er det første afsnit.

Lavpasfilter med Sallen-Key

Proceduren for at beregne filteret er, at der vælges nogle størrelser, hvor man så regner filteret igennem, og ser om det får en tilfredsstillende opførsel og nogle rimelige komponenter, ellers genvælges komponenter og der gennemregnes, indtil man får nogle komponenter der passer til kravene for filteret.

Udgangspunktet er følgende formler for et lavpasfilter:

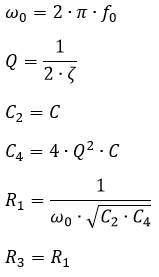
Formler til beregning af SallenKey Lavpas filter

Diagrammet for lavpasfilteret ser ud som følger:

Diagrammet til et SallenKey Lavpas filter

Ud fra et valg af kondensator-værdi C, fo og ζ eller Q kan man beregne komponenterne ud fra formlerne over diagrammet.

• Et Q på 0,7071 vil give en pæn karakteristik med -3dB ved knækfrekvensen.
• Et Q på 1 vil give 0dB ved knækfrekvensen, men en lille top inde i pasbåndet.
• Et højere Q vil give en større top.

Bestemmelse af komponenter og beregninger til et SallenKey Lavpas filter

Udtrykket opstilles ud fra reduktionen af kredsløbet, hvor operationsforstærkeren betragtes som ideel og modstande som impedanser Herefter indsættes de komplekse størrelser hvor der sidder kondensatorer. Dette giver følgende udtryk:

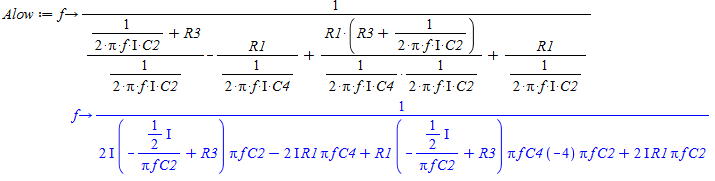
Udtrykket for overføringsfunktionen til et SallenKey Lavpas filter

For at kontrollere at filteret opfylder de ønsker vi har opstillet, så plottes grafen:

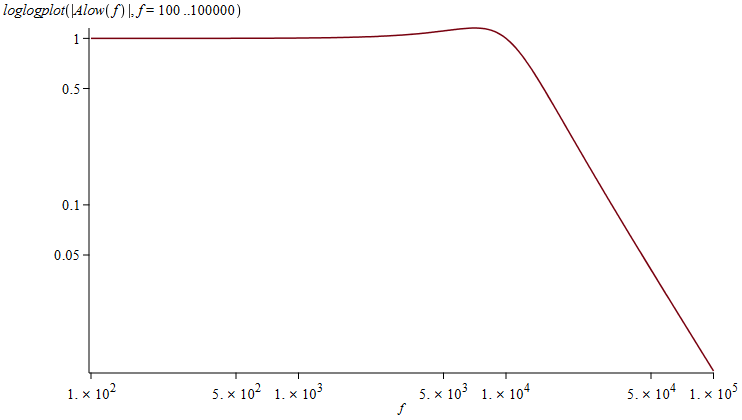
Frekvensgangen for et SallenKey Lavpas filter

Frekvensforløbet viser sig at have den ønskede form.

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen sallenKey.mw.

Højpasfilter med Sallen-Key

Proceduren for at beregne filteret er, at der vælges nogle størrelser, hvor man så regner filteret igennem, og ser om det får en tilfredsstillende opførsel og nogle rimelige komponenter, ellers genvælges komponenter og der gennemregnes, indtil man får nogle komponenter der passer til kravene for filteret.

Udgangspunktet er følgende formler for et højpasfilter:

Formler til beregning af SallenKey Højpas filter

Diagrammet for Højpasfilteret ser ud som følger:

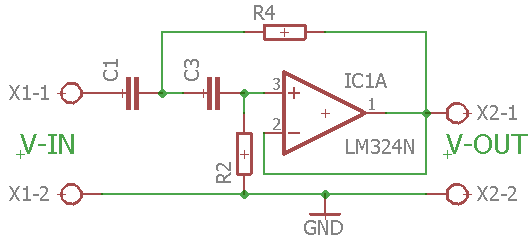
Diagrammet til et SallenKey Højpas filter

Ud fra et valg af kondensator-værdi C, fo og ζ eller Q kan man beregne komponenterne ud fra formlerne over diagrammet.

• Et Q på 0,7071 vil give en pæn karakteristik med -3dB ved knækfrekvensen.
• Et Q på 1 vil give 0dB ved knækfrekvensen, men en lille top inde i pasbåndet.
• Et højere Q vil give en større top.

Her vælges at filteret skal have -3dB ved knækfrekvensen

Bestemmelse af komponenter og beregninger til et SallenKey Højpas filter

Udtrykket opstilles ud fra reduktionen af kredsløbet, hvor operationsforstærkeren betragtes som ideel og modstande som impedanser Herefter indsættes de komplekse størrelser hvor der sidder kondensatorer. Dette giver følgende udtryk:

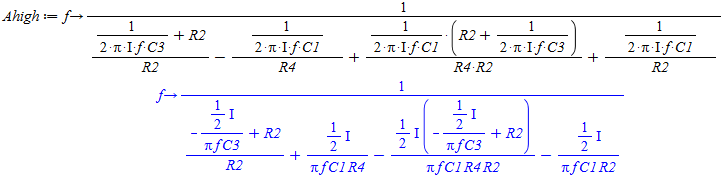
Udtrykket for overføringsfunktionen til et SallenKey Højpas filter

For at kontrollere at filteret opfylder de ønsker vi har opstillet, så plottes grafen:

Frekvensgangen for overføringsfunktionen til et SallenKey Højpas filter

Frekvensforløbet viser sig at have den ønskede form.

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen sallenKey.mw

Båndpas

Umiddelbart skulle man tænke, at det kunne lade sig gøre at lave et båndpasfilter med en Sallen-Key konfiguration, men det viser sig at det ikke giver nogen mening i grundkonfigurationen, så det springes over her.

Det kan lade sig gøre, når der kommer forstærkning i filteret, det kommer længere nede.

Sallen-Key Filtre med forstærkning

Det generelle layout for sådan et filter ser ud som følger:

Generel layout for et forstærket Sallen-Key Filter - impedanserne er modstande eller kondesatorer

Ved reduktion af udtrykket for de generelle impedanser kan man komme frem til følgende udtryk for forstærkningen:

Generelt udtryk for et forstærket Sallen-Key filter

Reduktionerne der er lavet for at beregne det generelle udtryk er lavet i PDF-filen andenOrdensReduktion, hvor dette er det andet afsnit.

Lavpasfilter med forstærket Sallen-Key

Proceduren for at beregne filteret er, at der vælges nogle størrelser, hvor man så regner filteret igennem, og ser om det får en tilfredsstillende opførsel og nogle rimelige komponenter, ellers genvælges komponenter og der gennemregnes, indtil man får nogle komponenter der passer til kravene for filteret.

Udgangspunktet er følgende formler for et lavpasfilter:

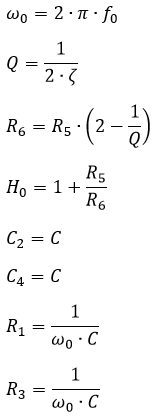
Formler til beregning af SallenKey Lavpas filter

Diagrammet for lavpasfilteret ser ud som følger:

Diagrammet til et SallenKey Lavpas filter

Ud fra et valg af kondensator-værdi C, fo og ζ eller Q kan man beregne komponenterne ud fra formlerne over diagrammet.

• Et Q på 0,7071 vil give en pæn karakteristik med -3dB ved knækfrekvensen.
• Et Q på 1 vil give 0dB ved knækfrekvensen, men en lille top inde i pasbåndet.
• Et højere Q vil give en større top.

Bestemmelse af komponenter og beregninger til et SallenKey Lavpas filter

Udtrykket opstilles ud fra reduktionen af kredsløbet, hvor operationsforstærkeren betragtes som ideel og modstande som impedanser Herefter indsættes de komplekse størrelser hvor der sidder kondensatorer. Dette giver følgende udtryk:

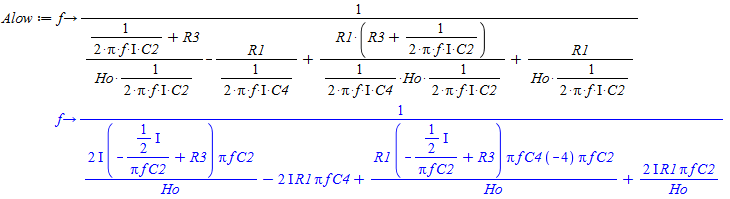
Udtrykket for overføringsfunktionen til et SallenKey Lavpas filter

For at kontrollere at filteret opfylder de ønsker vi har opstillet, så plottes grafen:

Frekvensgangen for et SallenKey Lavpas filter

Frekvensforløbet viser sig at have den ønskede form.

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen sallenKeyGain.mw.

Højpasfilter med forstærket Sallen-Key

Proceduren for at beregne filteret er, at der vælges nogle størrelser, hvor man så regner filteret igennem, og ser om det får en tilfredsstillende opførsel og nogle rimelige komponenter, ellers genvælges komponenter og der gennemregnes, indtil man får nogle komponenter der passer til kravene for filteret.

Udgangspunktet er følgende formler for et højpasfilter:

Formler til beregning af SallenKey Højpas filter

Diagrammet for Højpasfilteret ser ud som følger:

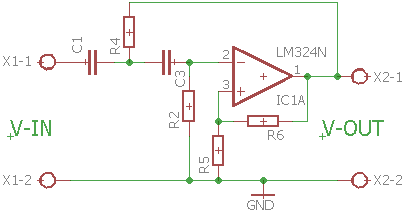
Diagrammet til et SallenKey Højpas filter

Ud fra et valg af kondensator-værdi C, fo og ζ eller Q kan man beregne komponenterne ud fra formlerne over diagrammet.

• Et Q på 0,7071 vil give en pæn karakteristik med -3dB ved knækfrekvensen.
• Et Q på 1 vil give 0dB ved knækfrekvensen, men en lille top inde i pasbåndet.
• Et højere Q vil give en større top.

Her vælges at filteret skal have -3dB ved knækfrekvensen

Bestemmelse af komponenter og beregninger til et SallenKey Højpas filter

Udtrykket opstilles ud fra reduktionen af kredsløbet, hvor operationsforstærkeren betragtes som ideel og modstande som impedanser Herefter indsættes de komplekse størrelser hvor der sidder kondensatorer. Dette giver følgende udtryk:

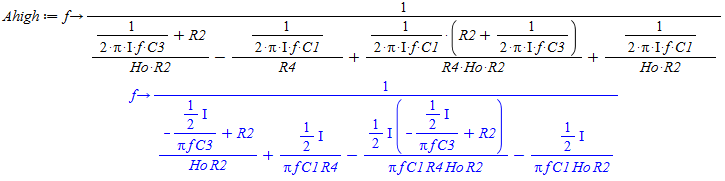
Udtrykket for overføringsfunktionen til et SallenKey Højpas filter

For at kontrollere at filteret opfylder de ønsker vi har opstillet, så plottes grafen:

Frekvensgangen for overføringsfunktionen til et SallenKey Højpas filter

Frekvensforløbet viser sig at have den ønskede form.

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen sallenKeyGain.mw

Båndpasfilter med forstærket Sallen-Key

Proceduren for at beregne filteret er, at der vælges nogle størrelser, hvor man så regner filteret igennem, og ser om det får en tilfredsstillende opførsel og nogle rimelige komponenter, ellers genvælges komponenter og der gennemregnes, indtil man får nogle komponenter der passer til kravene for filteret.

Udgangspunktet er følgende formler for et Båndpasfilter:

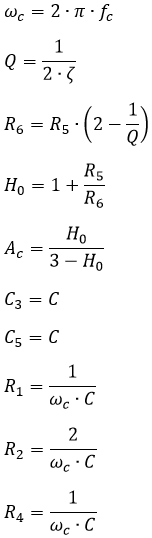
Formler til beregning af SallenKey Båndpas filter

Diagrammet for Båndpasfilteret ser ud som følger - som det kan ses, så er der kommet en ekstra modstand ind i filteret, hvilket betyder at beregningerne bliver lidt anderledes, men princippet er nogenlunde det samme:

Diagrammet til et SallenKey Båndpas filter

Ud fra et valg af kondensator-værdi C, fc og ζ eller Q kan man beregne komponenterne ud fra formlerne over diagrammet.

• Et Q på 0,7071 vil give en pæn karakteristik med -3dB ved centerfrekvensen.
• Et Q på 1 vil give et lille løft ved centerfrekvensen.
• Et højere Q vil give en større løft ved centerfrekvensen.

Der startes igen med at væle et Q, og her vælges Q=2, for at få en top på filteret:

Bestemmelse af komponenter og beregninger til et SallenKey Båndpas filter

Udtrykket er lidt anderledes end til Højpas og Lavpas, da der er en modstand mere - som impedanser ser det således ud:

Udtrykket som impedanser for et SallenKey Båndpas filter

Udtrykket opstilles ud fra reduktionen af kredsløbet, hvor operationsforstærkeren betragtes som ideel og modstande som impedanser Herefter indsættes de komplekse størrelser hvor der sidder kondensatorer. Dette giver følgende udtryk:

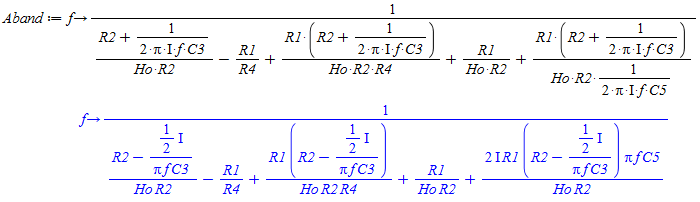
Udtrykket for overføringsfunktionen til et SallenKey Båndpas filter

For at kontrollere at filteret opfylder de ønsker vi har opstillet, så plottes grafen:

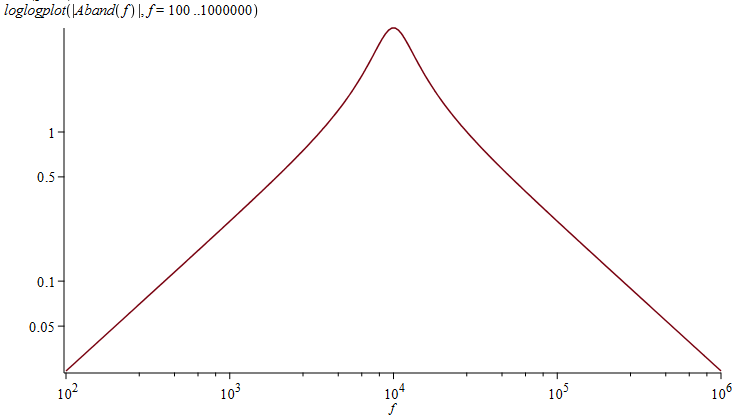
Frekvensgangen for overføringsfunktionen til et SallenKey Båndpas filter

Frekvensforløbet viser sig at have den ønskede form.

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen sallenKeyGain.mw

Multiple Feedback filtre

Denne type filter er kendetegnet ved at der sidder to impedanser i feedbacksløjfen, der giver ret store friheder, specielt til at designe filtre med et højere Q (en top omkring knækket/center).

Det generelle layout for sådan et filter ser ud som følger:

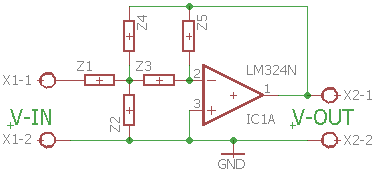
Generel layout for et Multiple Feedback Filter - impedanserne er modstande eller kondesatorer

Ved reduktion af udtrykket for de generelle impedanser kan man komme frem til følgende udtryk for forstærkningen:

Generelt udtryk for et Multiple Feedback filter

Reduktionerne der er lavet for at beregne det generelle udtryk er lavet i PDF-filen andenOrdensReduktion, hvor dette er det sidste afsnit.

Lavpasfilter med Multiple Feedback

Proceduren for at beregne filteret er, at der vælges nogle størrelser, hvor man så regner filteret igennem, og ser om det får en tilfredsstillende opførsel og nogle rimelige komponenter, ellers genvælges komponenter og der gennemregnes, indtil man får nogle komponenter der passer til kravene for filteret.

Udgangspunktet er følgende formler for et lavpasfilter:

Formler for komponenterne til et Multiple Feedback Lavpas

Diagrammet for lavpas-filteret ser ud som følger:

Diagrammet for et Multiple Feedback Lavpas Filter

Ud fra de tre størrelser H₀, ω0 og ζ, samt et valg af kondensator-værdi C og en faktor K beregnes komponentværdierne. (K vælges så kvadratrodstegnet bliver tæt på 0).

Kondensatorværdien til Multiple Feedback Lavpas Filter

C5 bliver til C, der er 1nF. K vælges så der kommer en rigtig størrelse på kondensatoren, Altså C2 bliver 22 nF K vælges samtidig så størrelsen under rodtegnet bliver positiv.

Konstanter til Multiple Feedback Lavpas Filter

ζ der her udtrykkes som z vælges så der kommer et vist løft på kurven lige omkring knækfrekvensen fo

Konstant til Multiple Feedback Lavpas Filter

Der vælges en forstærkning på 1,5, så der rammes efter en forstærkning på ca. 3 lige ved knækfrekvensen fo

Konstant og komponenter til Multiple Feedback Lavpas Filter

For at sikre at udtrykket under rodtegnet bliver tæt på 0, så beregnes det separat

Rodværdi til Multiple Feedback Lavpas Filter

Der beregnes både en a version af modstandene og en b version ud fra +/- før rodtegnet, for at kunne vælge den der giver mest realistiske modstande Ud fra R4a beregnes R1a og R3a - tilsvarende i b versionen

Komponentberegninger til Multiple Feedback Lavpas Filter

Der vælges a versionen, og de 3 modstande vælges til praktiske værdier

Praktiske værdier til Multiple Feedback Lavpas Filter

Udtrykket opstilles ud fra reduktionen af kredsløbet, hvor operationsforstærkeren betragtes som ideel og modstande som impedanser

Herefter indsættes de komplekse størrelser hvor der sidder kondensatorer. Dette giver følgende udtryk:

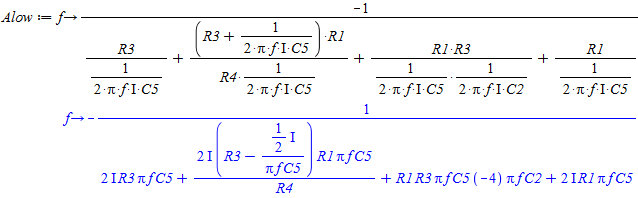
Udtrykket for Multiple Feedback Lavpas Filter

Plottet herunder efterviser at kurveformen ser ud som forventet

Graf over frekvensforløb til Multiple Feedback Lavpas Filter

Som det ses på grafen, så har frekvenskurven det forløb der ønskes.

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen multipleFeedback.mw.

Højpasfilter med Multiple Feedback

Proceduren for at beregne filteret er, at der vælges nogle størrelser, hvor man så regner filteret igennem, og ser om det får en tilfredsstillende opførsel og nogle rimelige komponenter, ellers genvælges komponenter og der gennemregnes, indtil man får nogle komponenter der passer til kravene for filteret.

Udgangspunktet er følgende formler for et Højpasfilter:

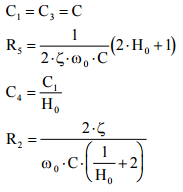
Formler for komponenterne til et Multiple Feedback Højpas

Diagrammet for højpas-filteret ser ud som følger:

Diagrammet for et Multiple Feedback Højpas Filter

Ud fra de tre størrelser H0, ω0 og ζ, samt et valg af kondensator-værdi C beregnes komponentværdierne.

Der vælges følgende:

Komponenter og konstanter der bestemmer Højpasfilteret

Ud fra dette beregnes:

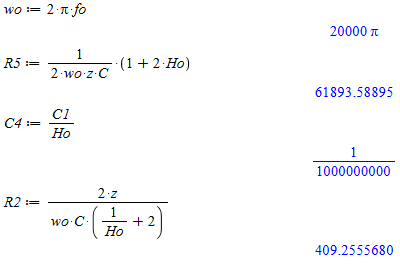
Beregning af Komponenter til Multiple Feedback Højpasfilteret

Følgende praktiske komponenter vælges:

Aktuelle Komponenter til Multiple Feedback Højpasfilteret

Udtrykket opstilles ud fra reduktionen af kredsløbet, hvor operationsforstærkeren betragtes som ideel og modstande som impedanser.

Herefter indsættes de komplekse størrelser hvor der sidder kondensatorer. Dette giver følgende oveføringsfunktion for filteret:

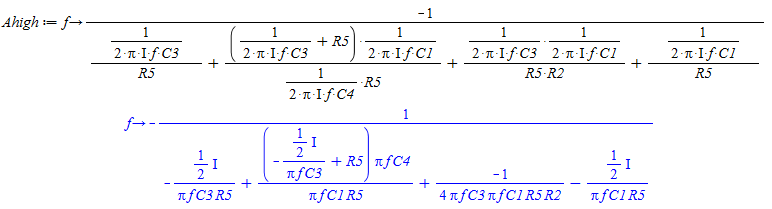
Udtrykket for Multiple Feedback Højpas Filter

Plottet herunder efterviser at kurveformen ser ud som forventet

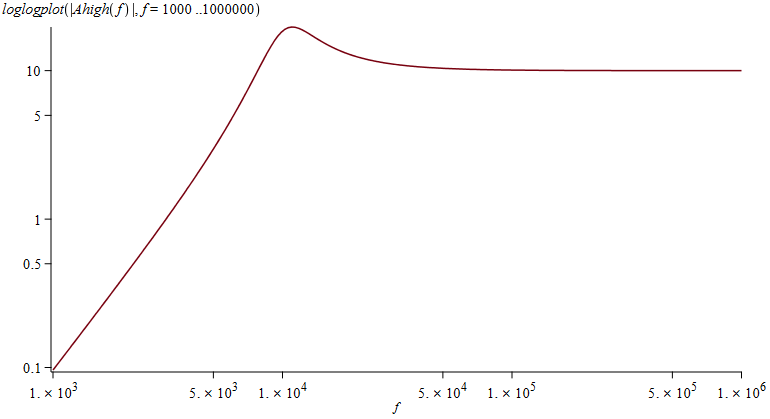
Graf over frekvensforløb til Multiple Feedback Højpas Filter

Som det ses på grafen, så har frekvenskurven det forløb der ønskes.

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen multipleFeedback.mw.

Båndpasfilter med Multiple Feedback

Proceduren for at beregne filteret er, at der vælges nogle størrelser, hvor man så regner filteret igennem, og ser om det får en tilfredsstillende opførsel og nogle rimelige komponenter, ellers genvælges komponenter og der gennemregnes, indtil man får nogle komponenter der passer til kravene for filteret.

Udgangspunktet er følgende formler for et Båndpasfilter:

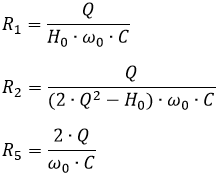
Formler for komponenterne til et Multiple Feedback Båndpas

Diagrammet for Båndpas-filteret ser ud som følger:

Diagrammet for et Multiple Feedback Båndpas Filter

Der vælges fo, Ho og enten BW eller Q, samt et valg af kondensator-værdi C for filteret:

fo der er centerfrekvensen, der hvor forstærkningen er højest - i midten af pasbåndet

Ho er forstærkningen i pasbåndet, nærmere bestemt ved fo

Der vælges en af de to næste størrelser, hvor den anden så udregnes fra

BW der er båndbredden eller forskellen mellem øvre og lave grænsefrekvenser - de steder hvor forstærkningen er faldet 3 dB

Q der er kvalitetsfaktoren, som er udtrykt ved fo / BW. Et lavt Q giver en stor båndbredde, et højt Q giver en smal båndbredde

Der vælges et rimeligt Q på 1,5, da vi ikke vil have ustabilitet ved centerfrekvensen

Der vælges en forstærkning på 2 ved centerfrekvensen fo

Komponenter og konstanter der bestemmer Båndpasfilteret

Kondensatoren C vælges til en fornuftig værdi - den skal tilrettes hvis modstandene enten bliver for store (over 1M) eller for små (under 100 ohm)

Kondensatorvalg og Beregning af Komponenter til Multiple Feedback Båndpasfilteret

Følgende praktiske komponenter vælges:

Aktuelle Komponenter til Multiple Feedback Båndpasfilteret

Udtrykket opstilles ud fra reduktionen af kredsløbet, hvor operationsforstærkeren betragtes som ideel og modstande som impedanser.

Herefter indsættes de komplekse størrelser hvor der sidder kondensatorer. Dette giver følgende oveføringsfunktion for filteret:

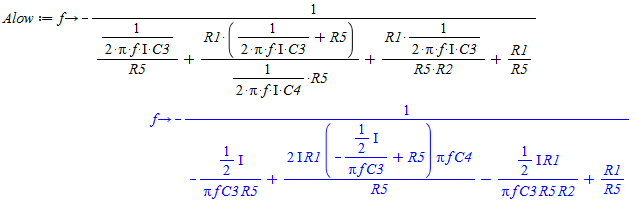
Udtrykket for Multiple Feedback Båndpas Filter

Plottet herunder efterviser at kurveformen ser ud som forventet

Graf over frekvensforløb til Multiple Feedback Båndpas Filter

Som det ses på grafen, så har frekvenskurven det forløb der ønskes.

Beregninger på eksempler på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen multipleFeedback.mw.

Kombination til højere ordens filtre

Der er forskellige typer filtre, der giver forskellige frekvensrespons, men også giver andre egenskaber over for fx. en steprespons eller et firkantsignal, men mest har det at gøre med formen på frekvensresponsen som illustreret her

Forskellige typer filtres frekvensresons (5. ordens)

Det at kombinere filtrene helt korrekt kræver at man kan regne i s-området, men man kan godt lave noget der minder om disse filter ud fra følgende kriterer:

Butterworth ligger med samme knækfrekvens, men der etableres et minimalt løft i alle 2. ordens led, så den samlede dæmpning i knækket bliver til 3 dB. De andre typer placerer knækfrekvenserne lidt forskelligt således at nogle filtre hæver og andre dæmper en del - dette er lidt mere kompliceret, da det kræver at man både rammer den rigtige frekevns og den rigtige mængde hævning i toppen - samtidigt skal toppene være højere for at kompensere for faldet fra de andre filtre, det giver større chance for ustabilitet. Dette stiger desuden med antallet af filtre i denne kombination, hvilket kræver noget præcisere komponenter.

Referencer

Filtre
Filtre	Aktive filtre - Komplekse tal - Sammenkobling af filtre - Butterworth - Chebyshev - Band-pass - RC-Led - Spole ved AC