Chebyshev filtre
| Et Chebyshev filter er et filter der realiseres, hvor man ønsker en god afskæring ved knækfrekvensen. Det har dog nogle omkostninger, så som dårlig tidsmæssig signalbehandling og at filteret ikke er jævnt i pasbåndet, men normalt vil have en form for ripler der.
Man kan realisere det på forskellig vis. Chebyshev, hvor man lægger knækfrekvensen forskellige steder. Man starter med et filter med stor godhed tæt på knækfrekvensen, og så lægger filtre med mindre og mindre godhed længere inde. På denne måde vil man få pukler i pasbåndet, men til gengæld også en stejl overgangs-kurve, der normalt har -3dB ved knækfrekvensen. Filtertypen har flere fordele, specielt at afskæringen i transientbåndet er meget skarp tæt på knækfrekvensen. En anden "pris" man betaler for dette ud over riplerne er at med den store godhed, så kommer man tættere på ustabilitet, så man skal være meget påpasselig med sine komponenter og med placeringen af komponenterne, så man ikke får selvsving. Med denne måde at dimensionere på bliver filteret også ret følsomt over for komponent-tolerancer, så ved større ordner af filteret kan man ikke helt stole på den teoretiske frekvensgang. |
Realisering af Chebyshev filtre generelt
Chebyshev filtre realiseres ud fra en række polynomier er der defineret i s-området, og som får parametre som følger:
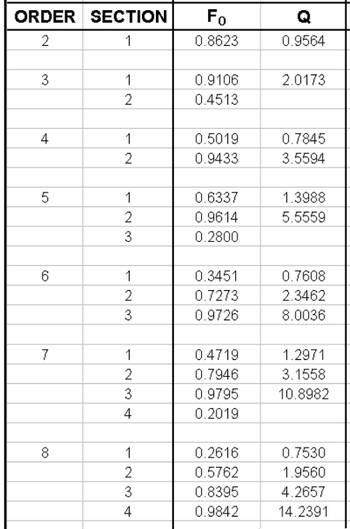
Polynomierne fra s-området til Chebyshev filtre op til 8. orden[1]
Det man kan se her er, at de ulige ordner (1. 3. 5. osv) har et 1. ordens led som et af elementerne, og så er der ellers koblet flere andenordens led sammen, men da konstanten på s2 ændrer sig, så er knækfrekvensen forskellig, og de har forskellige Q, som definerer komponentværdierne.
Beregninger på et 2. ordens led
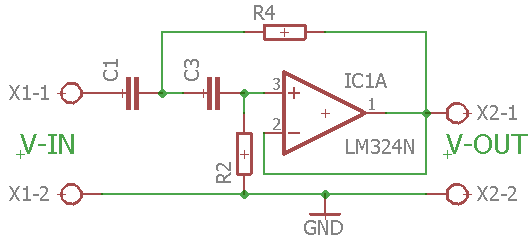
Der er forskellige måder at realisese 2. ordens led på, men her tages udgangspunkt i et Sallen-Key med unity gain, som ser således ud i et lavpas filter:

Diagrammet til et SallenKey Lavpas filer
For at beregne komponenterne skal man bruge konstanten fra s1 leddet, der for et 2. ordens filter hedder Q=0.9564.
Man skal også vælge en kondensator, som forsøges valgt ud fra hvilke frekvenser man arbejder med, men også ud fra praktiske hensyn, så man får en kondensator til en fornuftig pris. Herefter kan de resterende komponenter beregnes ud fra følgende:
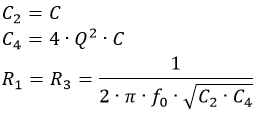
Formler til beregning af Sallen-Key Lavpas filter
Tilsvarende kan man realisere et højpas filter med et Sallen-Key filter på følgende måde:
Diagrammet til et SallenKey Højpas filter
Man vælger igen kondensatoren først, da kondensatorer ikke fås i så mange forskellige størrelser (i hvert fald ikke til en fornuftig pris), og man anvender samme Q fra s-udtrykket (som er gengivet i tabellen). Dette giver følgende beregninger:

Formler til beregning af Sallen-Key Højpas filter
Opbygning af 5. ordens filter
For at realisere et 5. ordens filter skal det bestå af 3 filtre efter hinanden, et 1. ordens og to 2. ordens, så den samlede orden bliver til 5. orden.
Det gennemregnede eksempel på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen 5orderChebyshev.mw.
Realisering af 5. ordens lavpas Chebyshev
Der vælges en forstærkning på 1, fordi hele filteret realiseres med Sallen-Key filtre og simple 1. ordens filtre. Der vælges en knækfrekvens på 3,3 kHz
Der tages udgangspunkt i s-udtrykket for et 5. ordens, hvor det vi skal bruge er de to konstanter og de 3 knækfrekvenser:

Polynomiet til et 5. ordens Chebyshev filter

Konstanterne til et 5. ordens Chebyshev filter
Første led - det 1. ordens filter
Første led realiseres med et 1. ordensfilter, der her skal ligge noget under knækfrekvensen
Først fastlægges selve filterets knækfrekvens fo
Ud fra fo beregnes de 3 knækfrekvenser, der er forskellige i de 3 filtre der indgår. f3 er knækfrekvensen for 1. ordens filteret og f1 og f2 er knækfrekvenserne til de to 2. ordens filtre.

Fastlæggelse af knækfrekvenserne til de 3 filtre
Der vælges en kondensatorværdi, her på 22nF, således at der kan bestemmes en modstand til 1. ordens leddet, og udtrykket for overføringsfunktionen kan bestemmes.

Beregningerne til det første filter
Andet led - det første 2. ordens filter
Det næste led realiseres med et 2. ordens Sallen-Key filter, det dimensioneres ud fra den angivne procedure, med knækfrekvensen f1 og med Q1 som den konstant der anvendes.

Diagrammet til et SallenKey Lavpas filter
Der vælges en kondensator, hvorefter resten af komponenterne kan bestemmes ud fra den beregnede knækfrekvens og det Q der er aflæst i tabellen. Der lægges 10 til komponentnavnene i det første filter, for at skille komponentbetegnelserne i de forskellige filtre fra hinanden.

Beregningerne til det andet filter
Tredje led - det andet 2. ordens filter
Ud fra den anden konstant Q2 og f2 beregnes på samme måde et andet 2. ordens Sallen-Key filter:

Diagrammet til et SallenKey Højpas filter
Der lægges 20 til komponentnavnene i det andet filter, for at skille komponentbetegnelserne i de forskellige filtre fra hinanden.

Beregningerne til det tredje filter
Kontrol af filteret
For at vise hvordan funktionerne spiller sammen laves et plot, hvor de 3 funktioner indgår:

Graf med de 3 led til det 5. ordens Chebyshev filter
Som det ses på kurverne, så har det ene 2. ordensfilter et ret stort løft (der stammer fra et stort Q) lige omkring knækfrekvensen for det endelige filter
For at se resultatet laves det samlede plot af den endelige funktion A(f), der er de 3 funktioner ganget sammen:

Graf med det samlede 5. ordens Chebyshev filter
Der ses på resultatet at filteret skærer ganske pænt lige omkring knækfrekvensen.
For at se filterets opførsel i pasbåndet laves et plot der kun lige går ud over knækket.

Graf med det samlede 5. ordens Chebyshev filter i pasbåndet
Her ses det ret tydeligt at der er ripler i pasbåndet.
For at eftervise at dæmpningen i knækket også ligger som forventet beregnes denne:

Kontrol af det samlede Chebyshev filters 3 dB punkt
Som forventet ligger den pænt på -3dB.
For at se hvilken indflydelse det har at bruge rigtige komponenter, så vælges komponenter til størrelser fra E12 rækken for modstandenes vedkommende, og for kondensatorerne forsøges at vælge fra E3 rækken, suppleret med enkelte fra E6 rækken.
Kondensatoren C14 laves som en parallelforbindelse af 22 og 15 nF.
Kondensatoren C24 laves som en parallelforbindelse af 100 og 22 nF.

Valg af reelle komponenter til Chebyshev filteret
Der laves et plot der viser frekvensgangen med de rigtige komponenter.

Graf med reelle komponenter i et 5. ordens Chebyshev filter i pasbåndet
Som det kan ses på grafen, så er der sket en del med pasbåndet, og karakteristikken er ikke så jævn som før, men i pasbåndet ligger udsvingene ikke meget over +/- 1 dB, så det er stadig acceptabelt.
For at eftervise at dæmpningen i knækket også ligger som forventet beregnes denne:

Kontrol af det reelle Chebyshev filters 3 dB punkt
Her ses at skævhederne har trukket den sidste top nedad, så knækfrekvensen dæmpes 1,5 dB ekstra. Det er en del, men stadig inden for et rimeligt acceptabelt område.
Det gennemregnede eksempel på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen 5orderChebyshev.mw.
Eksempel på dimensionering af højpas-filtre
Dimensioneringen er ikke dokumenteret her på siden, men der ligger en maplefil med eksempler på dimensionering af to højpas-eksempler, et 4. ordens og et 8. ordens.
Dimensioneringen er ikke dokumenteret helt igennem, men princippet er at finde de konstanter man skal anvende i tabellen, hvor det er Fo og Q man har brug for, så man kan dimensionere de 2. ordens filtre som det samlede filter består af. Beregningerne foretages ud fra følgende princip.
- Q indgår direkte i beregningerne.
- Fo er normeret til 1 Hz og et lavpasfilter i tabellen, så der tages reciprokværdien af Fo og der ganges med den ønskede frekvens.
- Der beregnes komponenter til alle de 2. ordens filtre der er angivet.
Det gennemregnede eksempel på filtrene ligger i Denne ZIP-fil med Maple Dokumenter i maple-filen Highpass4-8.mw.
Referencer
- ↑ Chebyshev Filterpolynomier tabel fra pdf med filterdesign, side 51.
| Filtre | |
|---|---|
| Filtre | Aktive filtre - Komplekse tal - Sammenkobling af filtre - Butterworth - Chebyshev - Band-pass - RC-Led - Spole ved AC |
