Komplekse tal
|
Et komplekst tal består af et reelt tal plus en størrelse af et imaginært tal, og det kan skrives således: k = a + b*i Her er a og b reelle størrelser mens i er det der gør leddet imaginært, og er defineret som kvadratroden af -1. Det at tage kvadratroden af -1 giver ikke umiddelbart mening, men ved at definere en størrelse, som ganget med sig selv giver -1, så kan vi omdanne tallinjen til et talplan, så et tal ikke blot er repræsenteret på en tal-linje, men i et helt plan. En ting man vil støde på når man læser om komplekse tal er at den imaginære størrelse i har forskellige betegnelser. I det meste af den matematiske litteratur kaldes den i, men i elektronik-litteratur bliver den tit kaldt for j, sikkert for at skelne den fra strøm der betegnes med i, og i Maple bruges et specielt I af ukendte årsager. |
Komplekse tal i elektronikken
Der hvor de komplekse tal giver rigtig god mening inden for elektronikken, er sammenhængen mellem komplekse tal og sinusfunktionerne, som er givet ved Eulers formel, som sætter en sammenhæng med svingninger.
Rent praktisk gør det, at vi kan anvende alle regneregler for strømme, spændinger og modstande, som Ohms lov og Kirchoffs love, hvis vi blot indfører kondensatorer og spoler som imaginære størrelser der er afhængige af frekvensen.
En kondensator får den imaginære størrelse 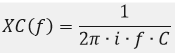
En spole får den imaginære størrelse ![]()
Dokumenter med beregninger i Maple ved hjælp af komplekse tal
Som nævnt kan Maple håndtere komplekse tal ved at man bruger et specielt I som den imaginære størrelse i sine beregninger.
Du kan finde de mapledokumenter der handler om komplekse beregninger i denne ZIP-fil med komplekse beregninger.
Der ligger forskellige typer filtre og forskellige eksempler i filen, denne sider tager udgangspunkt i filen komplekseKomponenter.mw.
RC-filtre betragtet ved hjælp af komplekse tal
En spændingsdeler med modstande kan tegnes på følgende måde, og man regner på den som vist ved efterfølgende eksempel:

beregninger fra Maple på en spændingsdeler
De 5V på indgangen af spændingdeleren bliver altså til 1.5625V på udgangen af spændingdeleren.
Et RC-led kan laves så det er både højpas og lavpas, og i begge tilfælde kan man betragte det som en spændingsdeler, men her bliver kondensatoren frekvensafhængig. For at kunne regne simpelt på RC-leddet så udtrykkes kondensatoren ved hjælp af imaginære tal, så kondensatorens "modstand" i beregningen i Maple bliver til:

Udtrykket for en kondensator, skrevet i Maple
Her er 2π blot en konstant, I er den imaginære størrelse der gør at det er komplekse tal vi arbejder med, f er frekvensen og C er størrelsen på kondensatoren.
RC Lavpas Filter
Et RC-led som lavpas ser ud som følger og hvis man vil beregne frekvensgangen, så indsætter man XC for "modstanden" der hvor kondensatoren er placeret:
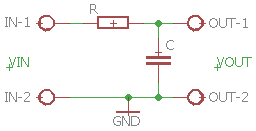
Lavpasfilter, hvor udgangspændingen tages ud over kondensatoren
Forholdet mellem Vout og Vin Vout/Vin kan i Maple udtrykkes som en funktion AlowpassRC ved at indsætte udtrykket XC i spændingdeleren, så man får følgende udtryk:
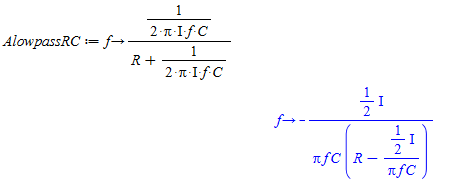
Udtrykket for et lavpas filer skrevet i Maple
For at lave et plot af frekvensgangen i Maple, så er man nødt til at plotte den nummeriske værdi, da man ikke kan plotte komplekse tal, og for at få et fornuftigt forløb laver man et dobbeltlogaritmisk plot af funktionen, hvilket kræver plot-pakken. Plottet ser ud som følger:
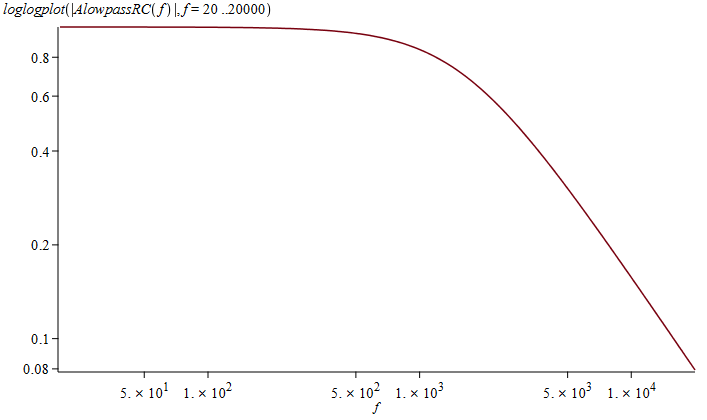
Plot af et RC lavpas-leds dæmpning som funktion af frekvensen
Det vi altså kan gøre med de komplekse tal er at vi kan opstille et generelt udtryk for overføringsfunktionen for en blanding af komponenter, hvor der også indgår kondensatorer, og beregne det for det ønskede frekvensområde, blot ved at anvende den teori vi kender fra jævnstrøms-teorien.
Mapledokumentet der beregner dette filter ligger i denne ZIP-fil i filen komplekseKomponenter.mw.
RC Højpas Filter
Ved at bytte om på R og C får man et Højpasfilter. Højpasfilteret ser ud som følgende diagram, om man kan udregne frekvensgangen på samme måde:
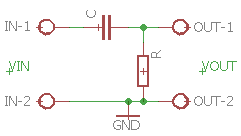
Højpasfilter, hvor udgangspændingen tages ud over modstanden
Forholdet mellem Vout og Vin Vout/Vin kan i Maple udtrykkes som en funktion AhighpassRC ved at indsætte udtrykket XC i spændingdeleren, så man får følgende udtryk:

Udtrykket for et højpas filer skrevet i Maple
For at lave et plot af frekvensgangen i Maple, så er man nødt til at plotte den nummeriske værdi, da man ikke kan plotte komplekse tal. Plottet ser ud som følger:
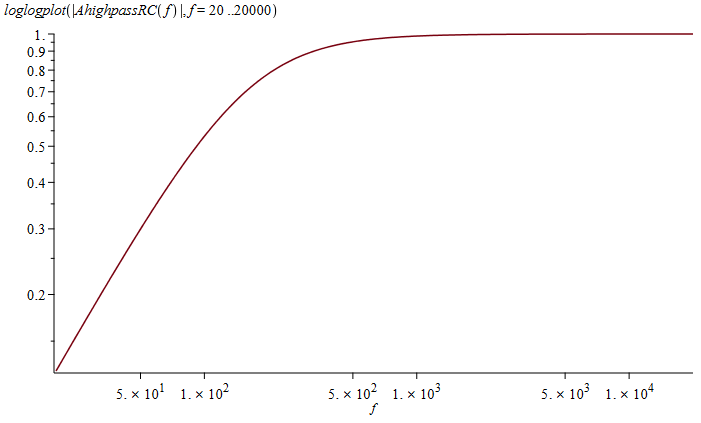
Plot af et RC højpas-leds dæmpning som funktion af frekvensen
Det generelle udtryk for overføringsfunktionen, hvor der indgår en kondensator, viser det ønskede frekvensområde, blot ved at anvende den teori vi kender fra jævnstrøms-teorien.
Mapledokumentet der beregner dette filter ligger i denne ZIP-fil i filen komplekseKomponenter.mw.
RL-led som Filter
På samme måde som en kondensator er frekvensafhængig, så er en spole også frekvensafhængig, blot på en anden måde. Dermed kan RL-led også lave både højpas- og lavpas-filtre
For at kunne regne simpelt på RL-leddet så udtrykkes spolen ved hjælp af imaginære tal, så spolens "modstand" i beregningen bliver til:
Det skal dog bemærkes at RL-led ikke er meget anvendte i elektronik-sammenhæng, da spoler er dyrere end kondensatorer, og de er også mere fysisk ustabile, så de har en højere fejlrate. På trods af dette anvendes de dog stadig i højtaleres passive delefiltre, specielt til bassen, hvor spolen kan stoppe de høje frekvenser og lade de lave frekvenser passere. I denne sammenhæng er modstanden normalt højtalerens egen modstand.
RL Lavpas Filter
Et RL-led som lavpas ser ud som følger og hvis man vil beregne frekvensgangen, så indsætter man XL for "modstanden" der hvor spolen er placeret:
Forholdet mellem Vout og Vin Vout/Vin kan udtrykkes som en funktion AlowpassRL ved at indsætte udtrykket XL i spændingdeleren:

Udtrykket for overføringsfunktionen for et RL-led som lavpasfilter
For at lave et plot af frekvensgangen i Maple, så er man nødt til at plotte den nummeriske værdi, da man ikke kan plotte komplekse tal. Plottet ser ud som følger:

Grafen for frekvensforløbet af et RL-led som lavpasfilter
Mapledokumentet der beregner dette filter ligger i denne ZIP-fil i filen komplekseKomponenter.mw.
RL Højpas Filter
Et RL-led som højpas ser ud som følger og hvis man vil beregne frekvensgangen, så indsætter man XL for "modstanden" der hvor spolen er placeret i spændingsdeleren:
Forholdet mellem Vout og Vin Vout/Vin kan udtrykkes som en funktion AhighpassRL ved at indsætte udtrykket XL i spændingdeleren:

Udtrykket for overføringsfunktionen for et RL-led som højpasfilter
For at lave et plot af frekvensgangen i Maple, så er man nødt til at plotte den nummeriske værdi, da man ikke kan plotte komplekse tal. Plottet ser ud som følger:
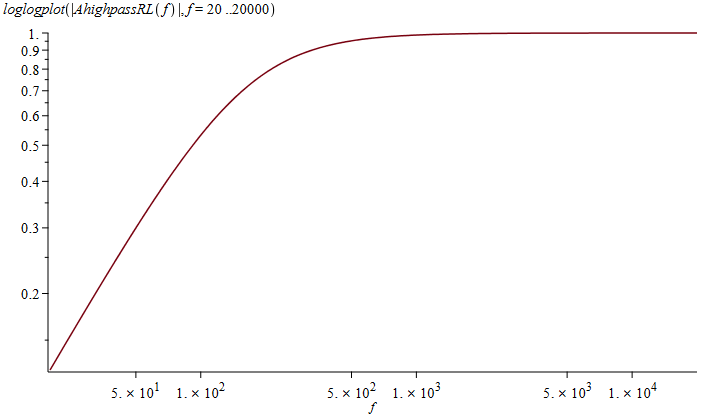
Grafen for frekvensforløbet af et RL-led som højpasfilter
Mapledokumentet der beregner dette filter ligger i denne ZIP-fil i filen komplekseKomponenter.mw.
Spole kondensator kombinationer
Ved at kombinere spoler og kondensatorer kan man lave forskellige typer filtre, hvor man fx. kan lade et filter lede en bestemt frekvens.
Her bestemmes blot "modstanden" Z gennem en kombination af en spole, en kondensator og en modstand der ser ud som følger:
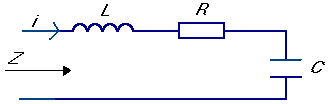
Kombination af L, R og C til en impedans med lav modstand ved centerfrekvens
"Modstanden", eller mere præcist Impedansen Z(f) beregnes som summen af XL, R og XC som følger:
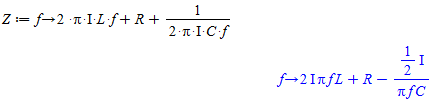
Udtryk for impedansen af RLC kombinationen
For at lave et plot af frekvensgangen i Maple, så er man nødt til at plotte den nummeriske værdi af impedansen, da man ikke kan plotte komplekse tal. Plottet ser ud som følger:
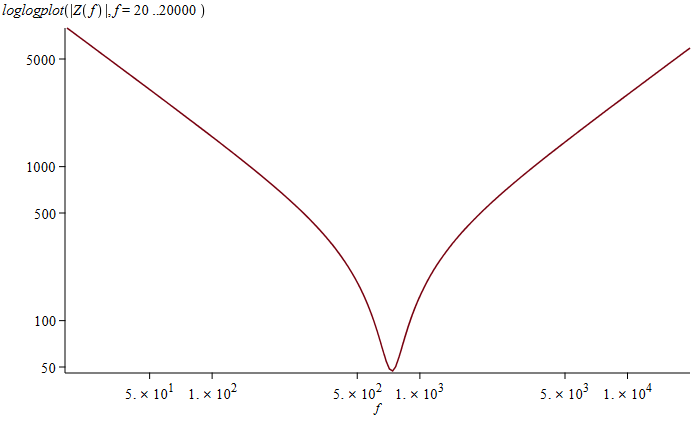
Graf der beskriver frekvensgangen for impedansen af RLC kombinationen
Mapledokumentet der beregner dette filter ligger i denne ZIP-fil i filen komplekseKomponenter.mw.
| Filtre | |
|---|---|
| Filtre | Aktive filtre - Komplekse tal - Sammenkobling af filtre - Butterworth - Chebyshev - Band-pass - RC-Led - Spole ved AC |



